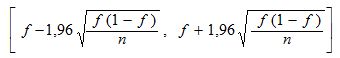Impact social de la mesure statistique
Georges Hoche
Nous avons rencontré M. Georges Hoche, inspecteur pédagogique régional (IPR) agrégé de mathématiques, qui a bien voulu répondre à quelques questions.
Nous : Les mathématiques jouent-elles un rôle dans l’élaboration des sondages ?
M. Hoche : Les sondages sont un élément omniprésent de notre vie démocratique. Il est donc intéressant d’étudier la place des mathématiques, appelées statistiques dans les sondages. Mais quelle est la place des mathématiques et plus précisément quelle est la place de la partie des mathématiques appelée statistiques dans les sondages ?
C’est une question qui concerne chaque citoyen, par exemple au moment des élections, moment où les sondages d’opinion prennent alors une place considérable dans l’actualité.
Les concepteurs des programmes scolaires l’ont bien compris quand ils ont introduit les statistiques dans les programmes ; on pouvait, il y a encore peu d’années, passer les concours pour devenir professeur de mathématiques ou encore intégrer l’école Polytechnique sans avoir jamais fait de statistiques (et très peu de probabilités) !
Pourtant, dès 1700, Jacques Bernouilli démontre la loi des grands nombres, puis Ronald A. FISCHER crée les bases de la théorie moderne de l'estimation.
Ce sera alors la naissance des instituts de sondage qui vont se servir à leur manière de ces supports théoriques : ainsi dès novembre 1936 quand F.D. Roosevelt remporte l’élection présidentielle aux Etats-Unis, le Literary Digest avait prédit la victoire de Landon sur 2.000.000 de personnes interrogées (par téléphone... d'où un biais) alors que George GALLUP avait annoncé celle de Roosevelt sur un échantillon aléatoire réduit. Son nom est devenu synonyme de « sondage d'opinion », et il sera à l’origine de la célèbre Gallup Organization.
Nous : Quelles sont les différentes techniques ? Sont-elles toutes aussi fiables ? Les mathématiques peuvent-elles aider à l’interprétation des sondages ?
M. Hoche : Il existe plusieurs méthodes permettant de réaliser des sondages :
- Tout d’abord le sondage aléatoire simple, qui est actuellement enseigné au lycée.
Il s’agit de tirer au hasard n éléments dans une population où la fréquence p d’un caractère est inconnue (par exemple le pourcentage p d’électeurs en faveur d’un candidat).
L’expression « au hasard » signifie que chaque échantillon de taille n a la même probabilité d’être tiré.
On peut facilement appliquer la théorie des probabilités à ce type de sondage.
Si n est « assez grand », des lois statistiques permettent de déterminer un « intervalle de confiance » : si on observe la fréquence f sur l’échantillon de taille n, on démontre que la fréquence correspondante inconnue p dans la population est située dans l’intervalle :
avec 95 % de « confiance ». Cette expression signifie que sur un grand nombre d’échantillons de taille n, dans environ 95 % des cas, p est effectivement dans l’intervalle ci-dessus.
- La deuxième méthode est le sondage par quotas.
C’est la méthode principalement utilisée par les instituts de sondages. Cette méthode ne contient rien d’aléatoire et par conséquent sa fiabilité ne peut être mathématiquement calculée, puisqu’on ne se sert pas du calcul des probabilités. La fiabilité de la méthode des quotas n’est qu’empirique, fondée sur « l’expérience des sondages précédents ».
La méthode des quotas consiste à choisir un certain nombre de critères jugés importants pour le sujet du sondage : sexe, âge, catégorie socioprofessionnelle, région, taille de la commune..., puis à calculer le pourcentage de personnes appartenant à chaque catégorie selon les données de recensement de l’INSEE.
Il s’agit alors d’obtenir autant de réponses que chaque quota ainsi calculé pour un échantillon de taille n. Évidemment des biais existent, en particulier parce que répondent les personnes joignables qui veulent bien répondre. C’est un peu comme si un biologiste voulant tester un nouveau produit sur une souris le faisait sur la première souris qu’il peut attraper dans la cage : il y a toutes les chances pour que cette souris soit la plus faible de toutes, la moins vive. Le grand avantage de la méthode des quotas est qu’elle ne nécessite pas de disposer d’une base de sondage d’où, comparativement à un sondage aléatoire de même taille, un très faible coût et une très grande rapidité. L’inconvénient est qu’il n’est pas possible de calculer la précision des estimations obtenues.
Nous : Peut-on évaluer la marge d’erreur ?
M. Hoche : Rappelons que pour la méthode des quotas, il est impossible d’évaluer sérieusement, c’est-à-dire mathématiquement, la marge d’incertitude.
Pour un sondage aléatoire simple de 1000 personnes, la marge d’incertitude à 95 % de confiance, à partir d’une fréquence f calculée sur le sondage, est de plus ou moins
Nous : Quels sont les éléments qui limitent encore la fiabilité des sondages ?
M. Hoche : Tout d’abord le taux de réponse (et de non réponse !)
La plupart des sondages sont effectués par téléphone. Dans ce cadre, le statisticien Michel Lejeune évoque un taux de réponse de l’ordre de 10% à 20%. Avec un tel taux de non-réponses, le biais est sans doute non négligeable. Qui répond ? Qui refuse de répondre ? Le taux de non réponse n’est sans doute pas le même dans les différentes catégories d’opinion.
Se pose également le problème des fausses déclarations.
C’est une source importante de biais pour des questions sensibles et souvent difficile à évaluer. Il existe des méthodes d’interrogation aléatoire, ou de recoupement avec d’autres questions. Enfin, le défaut de couverture est un autre biais important. La population sondée est-elle la population visée ? Si le sondage est effectué par Internet, s’il l’est par téléphone portable ou pendant les heures de travail, ... ce n’est certainement pas le cas. De toutes manières, des pans entiers de la population sont hors d’atteinte.
Nous : La moyenne est-elle l’unique outil mathématique ? Est-elle fiable ?
M. Hoche : Tout dépend de quel point de vue on se place! On peut faire dire un peu tout et n'importe quoi aux statistiques et autres sondages. De nombreux exemples sont révélateurs de la façon dont les journalistes peuvent nous mentir en jouant avec des chiffres, qu’ils interprètent parfois à leur façon. Par exemple, on a demandé à 1000 Français combien ils avaient d'enfants : la moyenne est de 2. On a demandé aussi aux enfants de ces 1000 personnes combien d'enfants ils sont dans leur famille. La moyenne des réponses est...3! On peut donc se demander s’il s’agit d’une erreur de calcul, ou alors si quelqu’un a menti ? Bien sur que non ! En fait, les enfants des familles nombreuses sont plus nombreux!!! Nous pouvons l’illustrer sur un exemple plus facile. On interroge alors deux parents : le premier a un enfant, le deuxième a trois enfants, donc la moyenne pour les parents est de (1+3)/2=2! Maintenant on interroge leurs enfants, ils sont au nombre de 4. L’un d’entre eux est un enfant unique, et les trois autres enfants sont trois dans leur foyer, la moyenne pour les enfants est donc : (1+3+3+3)/4=2,5.
Cela confirme bien qu’il faut s’interroger sur le point de vue où l’on se place.
Nous : Les sondages sont-ils toujours représentatifs de la population ?
M. Hoche : « Echantillon représentatif » : Voilà une expression qui, si elle n’est pas précisée, peut signifier à peu près n’importe quoi !
Un échantillon constitué selon la méthode des quotas est normalement « représentatif » des critères correspondants aux quotas (sexe, âge, catégorie socioprofessionnelle, région, taille de la commune...) selon lesquels il a été fabriqué. Mais on n’a aucun moyen de savoir jusqu’à quel point il est « représentatif » de ce pour quoi il a été prélevé, c’est-à-dire le sujet du sondage, l’opinion, le pourcentage que l’on cherche à évaluer. L’expression « représentatif de la population française », que l’on lit souvent dans la presse, prête évidemment à confusion. On a l’impression que l’échantillon est « représentatif » de tout ce que l’on veut.